Il mistero del diaframma
Vedremo oggi di risolvere un mistero riguardante il diaframma nel mondo fotografico.
Oggi vi propongo un articolo tecnico diverso dal solito: andremo a vedere cos’è, in ambito fotografico, il diaframma e come si rapporta alle altre entità (tempi, ISO) che formano l’esposizione. Risolveremo anche uno strano “mistero” legato al diaframma.
Innanzitutto: cos’è il diaframma?
Nelle fotocamere è indicato con: f/x, dove x è un numeretto (es. f/2.8 , f/4, ecc.) ed è il rapporto tra la lunghezza focale (f) e il diametro del foro attraverso il quale passa la luce.
Esempio: se abbiamo un’ottica 50mm e un diaframma f/4, significa che il diametro del foro di apertura è 50/4 = 12.5mm.
Per avere un’esposizione corretta (vedi articolo su Wikipedia) è necessario che tempi, ISO, diaframma siano nel giusto “rapporto”. Ad un incremento di un parametro deve corrispondere il decremento di un altro, ad esempio se i tempi si dimezzano (e quindi si dimezza la quantità di luce) dovrò raddoppiare gli ISO (devo raddoppiare la sensibilità del sensore).
L’azione di raddoppiare (o dimezzare) un valore si indica come “1 stop” di differenza.
ES: f/2, t=1 sec. ISO 6400 equivale a: f/2, t=2 sec. ISO 3200 (ho variato di +1 stop i tempi e -1 stop la sensibilità ISO)
Nel caso del diaframma, le cose non sono così facili, nel senso che variarlo di 1 stop non significa raddoppiare (o dimezzare) il numero f.
ES: f/2, t=1 sec. ISO 6400 equivale a: f/2.8, t=2 sec. ISO 6400 (ho variato di +1 stop i tempi e -1 stop il diaframma)
Faccio notare che una piccola differenza di f (da 2 a 2.8) ha significato un raddoppio (!!) dei tempi e questo vi fa capire, a titolo di esempio, quanto sia migliore un smartphone con lenti f/1.7 rispetto a un altro con lenti f/2.2.
Ma perché si passa da f/2 a f/2.8 (e non a f/4)?
Se avete avuto modo di modificare il diaframma nella vostra fotocamera (nei cellulari il valore è fisso), avrete visto una sequenza di questo tipo:
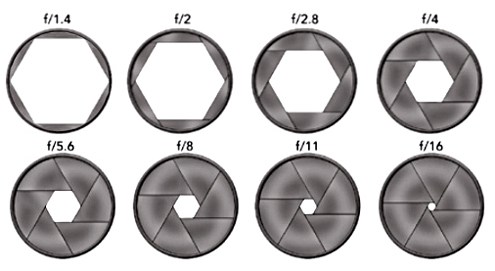
Da cosa dipende questa sequenza “misteriosa” e non lineare?
La colpa di tutto ciò è dovuta al fatto che il diaframma è legato alla misura di un’area e non di un’entità lineare. Infatti aumentare di +1 stop il diaframma equivale a raddoppiare l’area del foro di ingresso della luce.
Possiamo risolvere il “mistero” guardando questo schema e applicando un pò di geometria delle medie 😀 😀

Partiamo da un diaframma f/4 e vogliamo diminuire di 1 stop. Quanto sarà il nuovo diaframma?
Supponiamo che il foro di ingresso della luce non sia rotondo ma quadrato e che il diametro del cerchio sia il lato del quadrato (per i nostri calcoli è equivalente).
Avremo quindi un quadrato di lato 1/4 mm e area 1/16 mm2.
Diminuire di 1 stop significa dimezzare l’area di questo quadrato, quindi vogliamo arrivare ad un quadrato di area 1/32 mm2.
Il lato di questo quadrato è (vedi i calcoli) 1/5.6 (valore approssimato) e quindi il nuovo diaframma sarà: f/5.6.
Seguendo questa logica, possiamo costruire una tabella con tutti i valori di f all’incremento di 1 stop:
|
Diaframma
|
Valore di apertura del diaframma
|
Valore precisissimo
|
|
f/1
|
1
|
1/1
|
|
f/1.4
|
1/1.4
|
1/1,4142135623730950
|
|
f/2
|
1/2
|
1/2
|
|
f/2.8
|
1/2.8
|
1/2,8284271247461900
|
|
f/4
|
1/4
|
1/4
|
|
f/5.6
|
1/5.6
|
1/5,6568542494923801
|
|
f/8
|
1/8
|
1/8
|
|
f/11
|
1/11
|
1/11,3137084989847603
|
|
f/16
|
1/16
|
1/16
|
|
f/22
|
1/22
|
1/22,6274169979695207
|
|
f/32
|
1/32
|
1/32
|
|
f/45
|
1/45
|
1/45,2548339959390415
|
|
f/64
|
1/64
|
1/64
|
Con questo articolo spero di avere chiarito uno dei “misteri” della fotografia che numerosi fotografi alle prime armi incontrano nel loro percorso. Per qualsiasi altro dubbio o informazione vi aspetto nei commenti!






